直交座標と自然座標 - 科学のおもちゃ箱@Hatena

Yahoo! 知恵袋から拾った問題。直交座標と自然座標の比較研究のよい材料。
【問題】
鉛直平面（x-z平面）上のなめらかなスロープ $z=V(x)$ に沿う質量 $m$ の質点の運動を考える。
(1)　スロープに沿った運動において、力学的エネルギー保存を導出せよ。
(2)　スロープが $x$ 方向に一定の加速度 $a$ をもって運動するとき、スロープに固定された直交座標における運動方程式を導出せよ。
(3)　(2) の運動において質点がスロープから離れるときの条件を導出せよ。
f:id:yokkun831:20181221095949j:plain

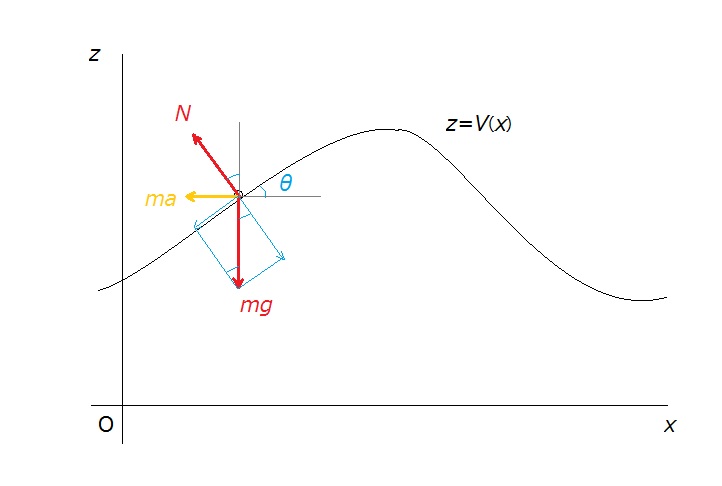
(1)　運動経路にそった「自然座標」を取るのが簡明である。
図のようにスロープの位置 $s$ における傾き角を $\theta$ とおくと、運動方程式は
$m\ddot{s} = - mg\sin\theta$
ここで、 $\sin\theta=\dfrac{dz}{ds}$ を適用して
$m\ddot{s} = - mg \dfrac{dz}{ds}$
両辺に $\dot{s}$ をかけて
$m\dot{s}\ddot{s} = - mg\dfrac{dz}{ds}\dfrac{ds}{dt}$
$\dfrac{d}{dt}\left(\dfrac{1}{2} m {\dot{s}}^2\right) = - mg \dfrac{dz}{dt}$
積分して力学的エネルギー保存を得る。
$\dfrac{1}{2} mv^2 + mgV(x) = const.$
ただし、 $v^2 = {\dot{s}}^2 = {\dot{x}}^2+{\dot{z}}^2$ 　である。

(2)　スロープに固定した直交座標系による運動方程式は、
$m\ddot{x} = - N\sin\theta - ma$
$m\ddot{z} = N\cos\theta - mg$
ただし、 $z=V(x)$ に沿った運動を考えるから、
$\dot{z} = \dfrac{dV}{dx}\dot{x}$
$\ddot{z} = \dfrac{d^2V}{dx^2}{\dot{x}}^2 + \dfrac{dV}{dx}\ddot{x}$
$\sin\theta = \dfrac{dz}{ds} = \dfrac{dz}{\sqrt{(dx)^2+(dz)^2}} = \dfrac{\dfrac{dV}{dx}}{\sqrt{1+\left(\dfrac{dV}{dx}\right)^2}}$
$\cos\theta = \dfrac{dx}{ds} = \dfrac{1}{\sqrt{1+\left(\dfrac{dV}{dx}\right)^2}}$
である。

(3)　(2)で得た運動方程式より $\ddot{z}, \ddot{x}$ を消去し、 $\dot{x}=v\cos\theta$ を考慮して $N$ について解くと、質点がスロープを離れる条件 $N<0$ すなわち
$V^{\prime\prime} v^2 - (1+{V^\prime}^2)(V^\prime a - g) \lt 0$
ただし、
$V^\prime=\dfrac{dV}{dx}, \quad V^{\prime\prime}=\dfrac{d^2V}{dx^2}$
を得る。

省略したが、垂直抗力を求めるこの計算はなかなかやっかいなシロモノである。そこで、結果の妥当性の検討を兼ねて、自然座標を用いて計算してみた。法線方向の運動方程式は、
$\dfrac{mv^2}{\rho} = mg\cos\theta - N - ma\sin\theta$
ここで、曲率半径は
$\rho = -\dfrac{(1+{V^\prime}^2)^{3/2}}{V^{\prime\prime}}$
である。ここから条件 $N<0$ が比較的容易に得られる。