ばね－質点系への衝突

剛体の回転・角運動量保存 振動 相対運動

思いつき問題。
【問題】
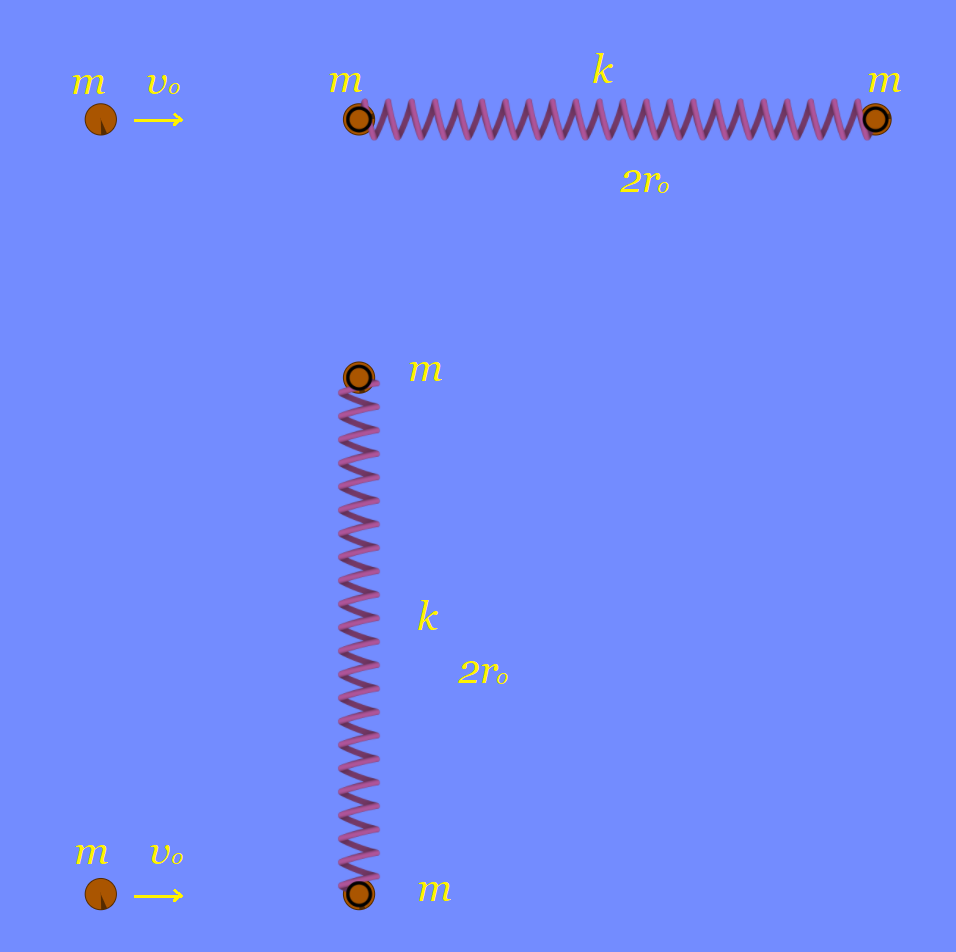
ともに質量 m の２質点がばね定数 k、自然長 2r_0 のばねでつながれ、なめらかな水平面上に静止している。質点の一方に同じ質量の質点を速さ v_0 で弾性衝突させる。ばね方向に正面衝突した場合と、ばねに垂直な方向に正面衝突した場合について、衝突後の系の運動を考察せよ。

f:id:yokkun831:20220322164601p:plain

Algodooシーンのダウンロード（衝突場面・重心系）
https://img.atwiki.jp/yokkun/attach/314/1504/bane-2mass-heno-shoutotsu1.phz
https://img.atwiki.jp/yokkun/attach/314/1505/bane-2mass-heno-shoutotsu2.phz

いずれの場合も衝突した質点は衝突後静止し、その後の運動に影響しない。
また、衝突後のばね－2質点系の重心速度は

V = \displaystyle\frac{v_0}{2}

となる。

(i) ばね方向への衝突

相対運動のエネルギー保存

\displaystyle\frac{1}{2}\mu (2\dot{r})^2 + \frac{1}{2}k\{2(r - r_0)\}^2 = {\rm const.}

ただし、r は重心から質点までの距離（ばねの長さの半分）、\mu = m/2 は換算質量である。

系は、重心速度 v_0/2 で並進しながら、重心まわりに角振動数

\Omega_0 = \displaystyle\sqrt{\frac{2k}{m}}

で単振動する。

(ii) ばねに垂直な方向への衝突

ばね－2質点系の重心まわりに対して角運動量保存

mr_0 v_0 = 2mr^2\omega

が成立する。すなわち、

\omega = \displaystyle\frac{r_0 v_0}{2r^2}

相対運動のエネルギー保存を用いてもよいが、運動方程式がより簡便かもしれない。

ばね方向の運動方程式

m\ddot{r} = -2k(r - r_0) + mr\omega^2

上の結果を適用すれば、

\ddot{r} = -{\Omega_0}^2(r - r_0) + \displaystyle\frac{{r_0}^2{v_0}^2}{4r^3}

\rho = r - r_0 とおくと、

\ddot{\rho} = - {\Omega_0}^2\rho + \displaystyle\frac{{r_0}^2{v_0}^2}{4(r_0+\rho)^3}

\rho\ll r_0 の条件の下で1次近似を実行すると、

\ddot{\rho} \simeq -\left({\Omega_0}^2 + \displaystyle\frac{3{v_0}^2}{4{r_0}^2}\right)(\rho - \rho_0)

の形を得る。

相対運動は変化する角速度 \omega の回転と、角振動数

\Omega \simeq \displaystyle\sqrt{{\Omega_0}^2 + \frac{3{v_0}^2}{4{r_0}^2}}

の振動の合成となる。

f:id:yokkun831:20220322173332p:plain
AlgodooシミュレーションとMathcad数値計算
f:id:yokkun831:20220322173424p:plain
Polymathによる数値積分結果